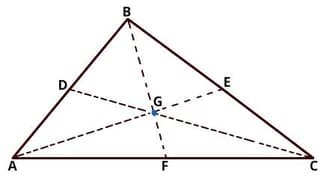
Medians of a Triangle

Let $BE$ and $CF$ be the two medians of a $∆\mathrm{ABC}$ and $G$ be their intersection. Also let $EF$ cut $AG$ at $O$. then find $AO : OG$.

In the given figure $\mathrm{BD}$is the angle bisector of angle $\mathrm{BD}$. What is the length of median drawn from B to $\mathrm{AC}$?

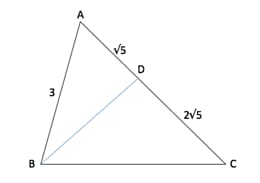
In the given figure $\mathrm{BD}$ is the angle bisector of angle $\mathrm{B}$. What is the length of median drawn from $\mathrm{B}$ to $\mathrm{AC}$?

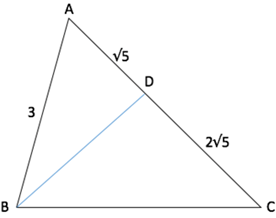
ABC is a triangle such that$\angle \mathrm{BAC} = 37.5º$ and $\angle \mathrm{BCA} = 62.5º,$ if BP is the median on AC, then the $\angle \mathrm{ABP}$ is

If the medians $\mathrm{AD}$ and $\mathrm{BE}$ of a triangle $\mathrm{ABC}$ intersect each other perpendicularly, and the vertices of the triangle are $\mathrm{A}(0,\mathrm{b}) \mathrm{B}(0,0) \mathrm{C}(\mathrm{a},0),$ then the relationship between $\mathrm{a}$ and $\mathrm{b}$ will be

Identify the triangles whose all the medians and heights (altitudes) are same.

The three medians $\mathrm{AX}, \mathrm{BY}$ and $\mathrm{CZ}$ of $△\mathrm{ABC}$ intersect at point $\mathrm{L}$. If the area of $△\mathrm{ABC}$ is $30 {\mathrm{cm}}^2$, then the area of the quadrilateral $\mathrm{BXLZ}$ is:

Length of each side of an equilateral triangle is $4 \mathrm{cm}$. If the length of median is $k\sqrt{3} \mathrm{cm}$, find the value of $k$.

Identify the type of segment required in the below triangle:

$BD=$

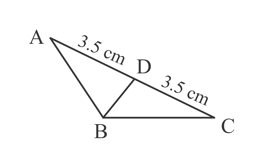
 Given $AM$ is the median, which of the following statements is false?

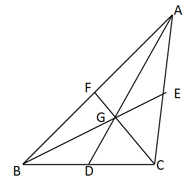
 $G$ is the centroid of triangle $ABC$ and $BF=10$. If the length of $FA$ is $x$ then find $x$.

 Which of the following describes a median of a triangle?

In $△ABC,$ the median $AD, BE$ and $CF$ passes through the point $G$. If $AD=7.5 \mathrm{cm},$ then find $GD$ (in $\mathrm{cm}$) (correct up to one decimal place)

In $△ABC,$ the median $AD, BE$ and $CF$ passes through the point $G$. If $GF=4 \mathrm{cm}$ then, find $GC$ (in $\mathrm{cm}$).

If A and B are midpoints of side RP and RQ of a triangle respectively (which is right angled at R); then the value of $4(A{Q}^2+B{P}^2)$ is :-

Choose the correct option:

A median of a triangle is the

The point of concurrence of the medians of a triangle is called

Are the medians of a triangle concurrent?

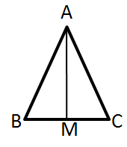
In which triangle is the median perpendicular to the base?

In which triangle is the median perpendicular to the base?